Learn One Thing A Day

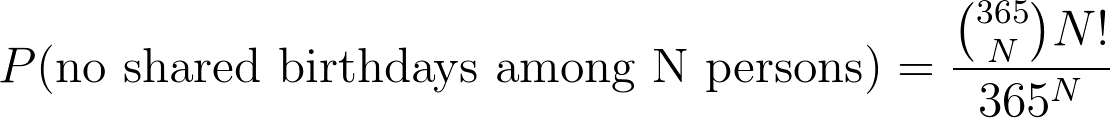
The birthday problem (or birthday paradox) refers to the probability that, in a group of N people, there is at least one pair of people having the same birthday. Surprisingly, you need just 23 people to have more than 50% chances to find at least a pair! Yes, only 23! Not, as you could think, 183! There are a short and a long versions of this post. The short one ( aka what you have to remember to impress your friends ) is: In a room with 23 people there are more than 50% chances (50.73% to be precise) to have a at least a couple sharing their birthday.  With 50 people, the probability is 97.04 % and with 80 people we arrive to 99.99% changes to find such  a couple! How is that possible? The rest of the post (the long version) proves the previous numbers. First of all, we have to make some basic assumptions: We have no twins in the room.  No one is born on February, 29th! (we do not consider leap years) Every day is as good as all the others.   In ...

There is always some madness in love. But there is also always some reason in madness. (source: wikipedia ) Friedrich Nietzsche (1844 - 1900), " On Reading and Writing " Nietzsche was a German philologist, philosopher, cultural critic, poet and composer.

Good judgement comes from experience. Experience comes from bad judgement. Jim Horning (1942 - 2003), American computer scientist. Quite true!

All that is necessary for the triumph of evil is that good men do nothing. This very nice and famous quote is attributed to Edmund Burke (1729-1797) an Irish political philosopher and statesman. However, wikipedia says something interesting about it: This is probably the most quoted statement attributed to Burke, and an extraordinary number of variants of it exist, but all without any definite original source. These very extensively used remarks may be based on a paraphrase of some of Burke's ideas, but he is not known to have ever declared them in so succinct a manner in any of his writings. They may have been adapted from these lines of Burke's in his Thoughts on the Cause of Present Discontents (1770): "When bad men combine, the good must associate; else they will fall one by one, an unpitied sacrifice in a contemptible struggle." Anyway, I definitely agree with the content of the sentence, whatever its origin is.

Today I want to discuss a tip that can be very useful in the kitchen. How can you test if an egg is fresh or, at least, still eatable? There are some ways to check it but the one I like the most is the sinking test. Take a transparent bowl and fill it with some cold water. It can be also a big glass, but it's important that you can see through it. Put your egg *gently* in the water. Now, three things can happen: A) if the egg sinks to the bottom, it's fresh. Very fresh! B) if the egg sinks but stands on its point, it is about 7 days old and it's still eatable. C) if the egg floats to the top, guess what?, you have to throw it away. To make everything clearer I made I nice drawing :) (source: myself ) This test works because the egg shells are porous and over time the liquid inside slowly evaporates ( being replaced by the air) making the egg buoyant. As I told you, this is not the only way to test egg freshness, but it's the one I like the most. ...

Patience has its limits. Take it too far, and it's cowardice. George Jackson (1941 - 1971)

"Example is not the main thing in influencing others. It is the only thing." Albert Schweitzer (1875-1965) theologian, organist, philosopher, physician, and medical missionary.

The whole sense of the book might be summed up the following words: what can be said at all can be said clearly, and what we cannot talk about we must pass over in silence. Ludwig Wittgenstein (1889 – 1951) was an Austrian-born philosopher who spent much of his life in England.

There are in fact two things, science and opinion; the former begets knowledge, the latter ignorance. Hippocrates (460 BC - 377 BC), an ancient Greek physician of the Age of Pericles (Classical Greece),  and is considered one of the most outstanding figures in the history of medicine.

Today I learned that there is a star, called HD 140283 , or more easily, the " Methuselah Star " or the " Genesis Star " that appears to be old just as the Univese itself! (Image from Wikipedia ) It is 190.1 light-years away, its size is 1.4 times the Sun and it's age is 14.46 ± 0.8 billions of years. As stated, its age is pretty impressive, condisidered that the age of the Universe is only 13.798 ± 0.037 billions of years! Within the error bars, this star is just old as the Universe itself!!! The star must have formed soon after the Big Bang, and it has perhaps the largest age purported to any star. Other info about the Mathuselah are available at the wikipedia link .

Science may set limits to knowledge, but should not set limits to imagination. Bertrand Russell (1872 - 1970)

We already know ( right? ), that an adult human body has 206 bones, (babies have about 300), but did you know that 26 bones are located in each foot and ankle, i.e. 25% of ALL your bones are actually in your feet! (52/206=25.2 %)!!! (source wikipedia ) These bones contain in 33 joints (per foot), with over one hundred muscles, tendons, and ligaments in each foot also! Read more at http://www.omg-facts.com/Science/25-of-your-bones-are-located-in-your-fee/34895#QdL2SvlXIDw04Wm4.9 The human body contains 206 bones total. 26 bones are located in each foot and ankle, meaning that there are 52 bones altogether in your feet. That’s a quarter of the total bones in your body! Read more at http://www.omg-facts.com/Science/25-of-your-bones-are-located-in-your-fee/34895#QdL2SvlXIDw04Wm4.99 The human body contains 206 bones total. 26 bones are located in each foot and ankle, meaning that there are 52 bones altogether in your feet. That’s a quarter of the total bones in your body! Read m...

Today I learnt that the English word Palace ( but the same applies for Palazzo , (Italian), Palais (French), Palast (German)  etc) comes from the Latin Palātium , that is the name of one of the seven hills of Rome (Palatine in English). Long after the city grew to the seven hills the Palatine remained a desirable residential area. Emperor Caesar Augustus lived there in a purposely modest house only set apart from his neighbours by the two laurel trees planted to flank the front door as a sign of triumph granted by the Senate. His descendants, especially Nero, with his "Golden House" enlarged the house and grounds over and over until it took up the hill top. The word Palātium came to mean the residence of the emperor rather than the neighbourhood on top of the hill. (source wikipedia )

To be conscious that you are ignorant is a great step to knowledge. Benjamin Disraeli (1804 - 1881) British Conservative politician, writer, aristocrat and dandy who twice served as Prime Minister.

Today I learnt that pineapple is a compound fruit! It is indeed composed of many diamond-shaped fruitlets fused together! Each of these fruitlets comes from a small purple flower that blooms only one day! Could you imagine that?! (wonderful image from insidenanabreadshead.com ) By the way, do you remember that pineapple grow quite close to the ground ?

"Tis better to have loved and lost / Than never to have loved at all" This is another English commonplace that is actually a quotation of the English poet Alfred Tennyson, 1st Baron Tennyson (1809-1892). (source: wikipedia ) Other quotes are available here: Lord Tennyson . Stay tuned!

After all is said and done, a hell of a lot more is said than done. Slashdot

There is a book, a wonderful book, that I warmly recommend you, it's A short history of (nearly) everything by Bill Bryson . It's one of the best book on science I have ever read! Written by a journalist, who at a certain point in his life, decided to learn more about our planet and about about science in general and full of anecdotes. Today I want to tell you about the deepest borehole, one of the stories Bill Bryson tells in his book. By the 1960s scientists had grown sufficiently frustrated by how little they understood of the Earth’s interior that they decided to try to do something about it. Specifically, they got the idea to drill through the ocean floor (the continental crust was too thick) to the Moho discontinuity and to extract a piece of the Earth’s mantle for examination at leisure. The thinking was that if they could understand the nature of the rocks inside the Earth, they might begin to understand how they interacted, and thus possibly be able to predict...

All men by nature desire knowledge. Aristotle (384 BC - 322 BC), Metaphysics

Happy dogs wag their tails more to the right (from the dog's point of view), while nervous dogs have a left-dominated swish and fellow canines can spot (and respond) to these subtle tail differences, a study in Current Biology   reports. Canines that see tails wagging to the right are more relaxed, whereas they become more stressed when they see tails wagging to the left.  (source: Psychology Today ) Resources: BBC National Geographic Psychology Today

The most exciting phrase to hear in science, the one that heralds new discoveries, is not "Eureka!" (I found it!) but "That's funny ..." Isaac Asimov (1920-1992), American author and professor of biochemistry at Boston University, best known for his works of science fiction and for his popular science books.

What Francis Scott Key Fitzgerald (American Writer - The Great Gatsby ), Martin McFly (the fictional character in  Back to the Future ) and Sara O'Connor (fictional character in Terminator ) have in common? Well all of  them have a patronymic as surname. Indeed Fitzgerald and McFly mean indeed " Son of Gerald " and " Son of Fly " respectively. O'Connor  is slightly different, meaning grandson/descendant of Conchobhar (an Irish male name). The "Mac" or "Mc" versions have Scottish origin, while Fitzgerald is English being Fitz closely related to the French " fils " meaning Son same for O' being an abbreviation for " of ". Other patronymic are pretty obvous as the English surnames ending by "son" like Carlson. Many other patronomymics are listed on this wikipedia page.

"Knowledge comes, but wisdom linger" this English commonplace is actually a quotation of an English poet, Alfred Tennyson, 1st Baron Tennyson (1809-1892). (source: wikipedia ) There are other English commonplaces are actually Lord Tennyson 's phrases as you'll see in later posts on the blog! Stay tuned!

On OSX, Preview, by default, displays the last page you have read when you open a pdf. This is a pretty handy feature when you start reading a long pdf and do not want to search manually for the last page when you re-open the file. Today I found out how to easily set this behavior even on Acrobat Reader. Just launch Acrobat Reader and go to the menu Edit-> Preferences... , In the new window that will prompt, select the category Documents and check the option Restore last view settings when reopening documents available under the tab Open Settings. That's it. Enjoy your readings.

Science is organized knowledge. Wisdom is organized life. Immanuel Kant (1724 - 1804)   (source philosophers.co.uk )

Today I have learnt that the little pocket on the right-hand side of a pair of jeans is called watch pocket . (source: http://www.fcaministers.com/ ) It was invented in the late 1800s by Levi Strauss (1829-1902), to help cowboys storing their watches. Nowadays it used for different purposes as to keep coins and for this reason it is also called coin pocket.

Why do you need an alternative to Google Search? Just one word: privacy! The alternatives below work very well as search engines and do respect your privacy. If you care about privacy. https://www.ixquick.com/ and https://startpage.com/ http://duckduckgo.com/

"The whole problem with the world is that fools and fanatics are always so certain of themselves, but wiser people so full of doubts." (source marxists.org ) Bertrand Arthur William Russell (1872-1970), British nobleman, philosopher, logician, mathematician, historian, and social critic.

Today I learnt that the famous saying " one swallow does not make a summer " is a quotation of Aristotle (384-322 BCE) and is contained in his work The Nicomachean Ethics. In addition, it is part of a much longer and nicer sentence:   One swallow does not make a summer, neither does one fine day; similarly one day or brief time of happiness does not make a person entirely happy. (Roman copy in marble of a Greek bronze bust of Aristotle by Lysippus, c. 330 BCE. The alabaster mantle is modern. From wikipedia )

Have you ever wondered why your fingers wrinkle when you do the washing-up?   (source: http://www.bbc.co.uk/news/ ) As surprised as you might be, it seems that only recently scientists have found an explanation for this phenomenon. According to researchers of the New cast le University , it could be the results of evolutionary development.  The shrivelling of the skin on the fingers makes it easier to grip things underwater and pick up wet objects!  Researcher Tom Smulders said: ‘Going back in time, this wrinkling of our fingers in wet conditions could have helped with gathering food from wet vegetation or streams.’ (source: dailymail.co.uk ) So, when you do the washing-up without gloves and your fingers get wrinkled, it's just your body telling you " Sir, can I impro ve your grip o n th at soapy dish of yours ?"  The small comic strip below seems perfect to close this post :)  (source: dailymail.co.uk )

The length of your foot is the same as the length of your forearm. Read more at http://www.omg-facts.com/Science/The-length-of-your-foot-is-the-same-as-t/13349#mpyMaphOBphj7X85.99 The other day I was lazily watching the beginning of Pretty Woman in TV, in my defence I want just something to hear while I was preparing my dinner :) Anyway, at some point during the movie, a statement made by Vivian Ward (i.e. Julia Roberts) got my attention. She said to Edward Lewis (i.e. Richard Gere): "You know, your foot's as big as your arm from your elbow to your wrist?" As you are probably doing, I tested it immediately :) and it is true! It turns out that, through the anthropometry (i.e. the study of the measure of the human body parts and their ratios), this is not the only amazing thing about the human body! The study of the proportions is a quite ancient thing... do you know the famous Leonardo's Vitruvian Man? (from wikipedia ) Ah, there are also other int...